Houdini - Rotations and Look At
A point doesn’t “point” anywhere. Points have no implicit direction or orientation. The idea of “rotating a point” is essentially meaningless.
1. When we “rotate a point”, we are implicitly saying “translate this point around the origin”.
Take this example of “rotating” points in a Point Wrangle:
matrix3 m = ident();
rotate(m, @Time, {0, 1, 0}); // Rotate on Y over @Time
@P *= m;
What we’re really doing is translating points around the origin:
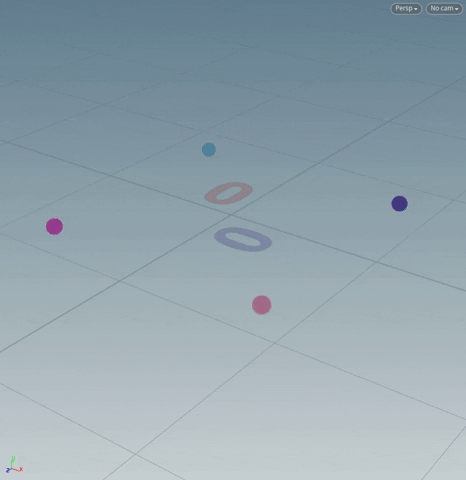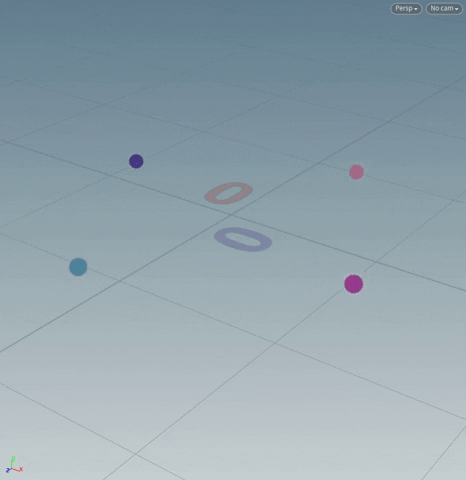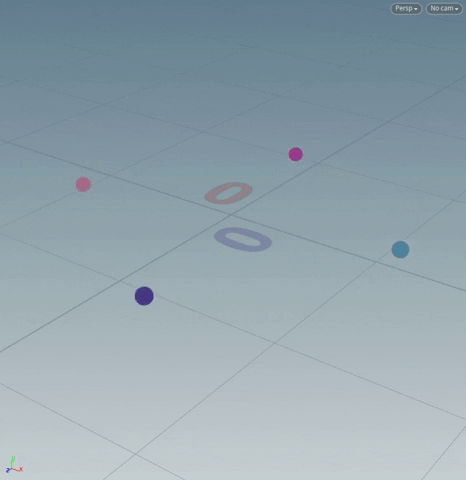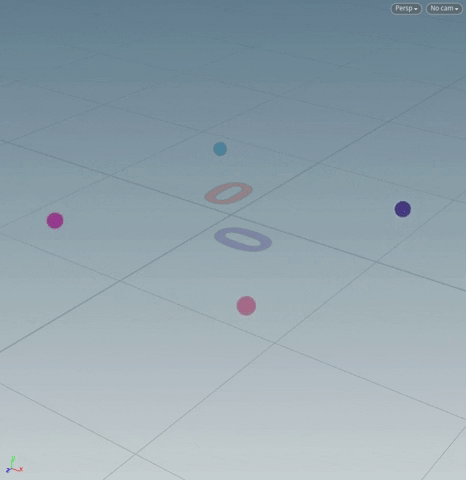
[If we think of points as vectors extending from the origin, we are simply rotating those vectors around the origin.]
The origin is always the implicit frame of reference for all transformations (scale, rotate, translate) – unless we can specify a pivot (which we’ll do later on).
2. To “rotate a primitive” is to translate the points of that primitive.
Since there can be no primitive without points, rotating/transforming the points of a primitive has the effect of rotating/transforming the primitive.
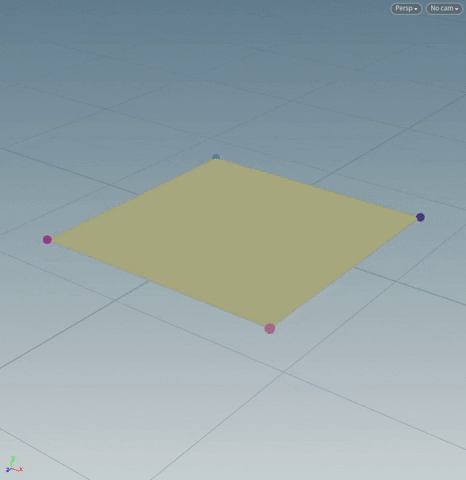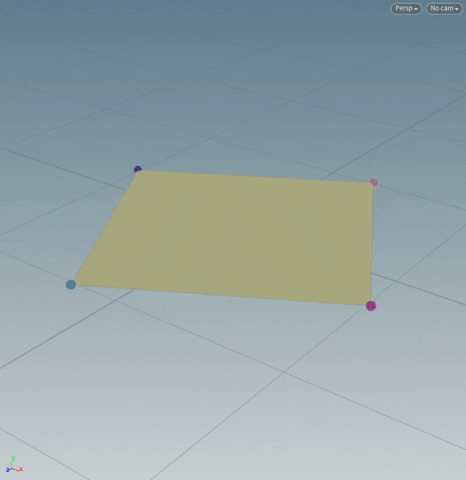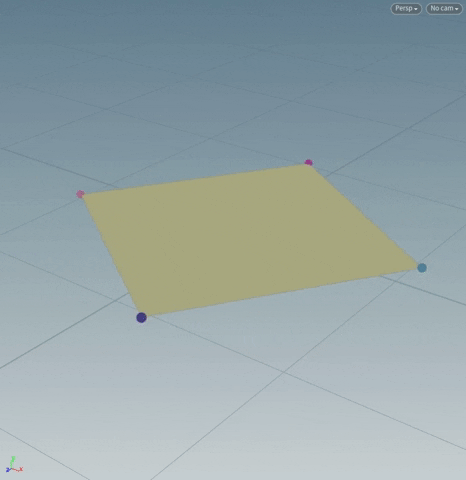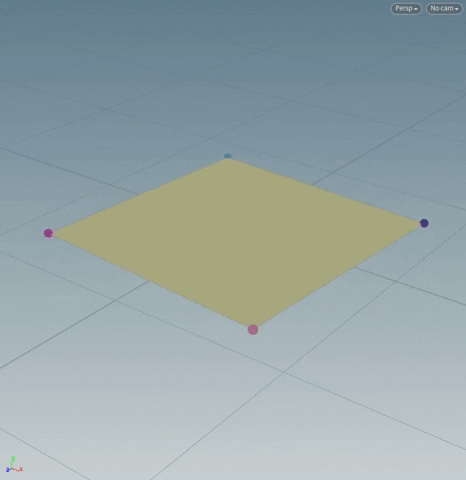
3. The “center” of a polygonal primitive is the averaged position of all its points' positions.
The center is usually where the normal “shoots out” from. In a Primitive Wrangle, @P refers to this “center”:
vector positions[];
foreach(int pt; primpoints(0, @primnum)) {
push( positions, point(0, "P", pt) );
}
@P == avg(positions); // is "usually" true or thereabouts
When we rotate the points of a primitive, we use this “center” as the pivot for all transforms.
Note also, the “normal” of a primitive is the average of all its points' normals.
Look At
The main idea of getting A to “look at” B is to first find a “target vector” that extends from A to B, and then rotating A to align with that target vector.
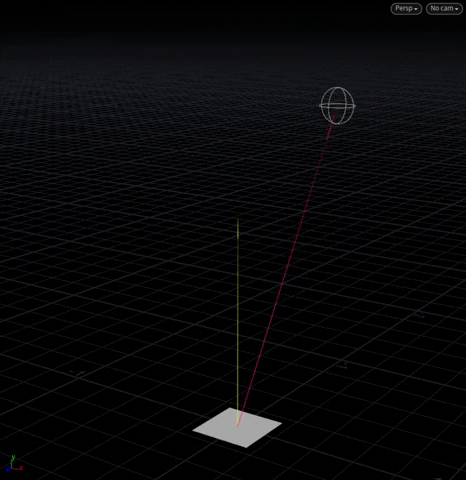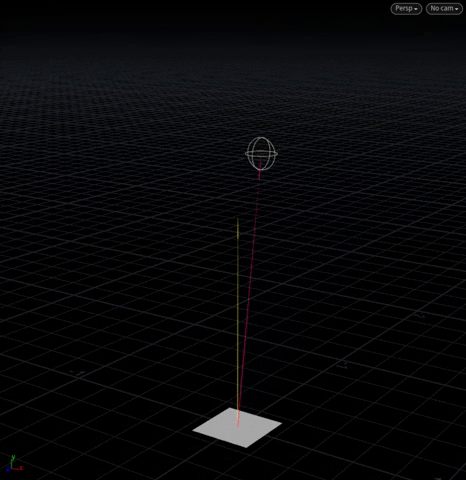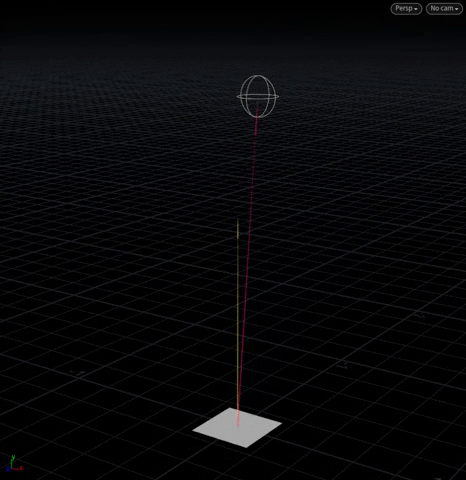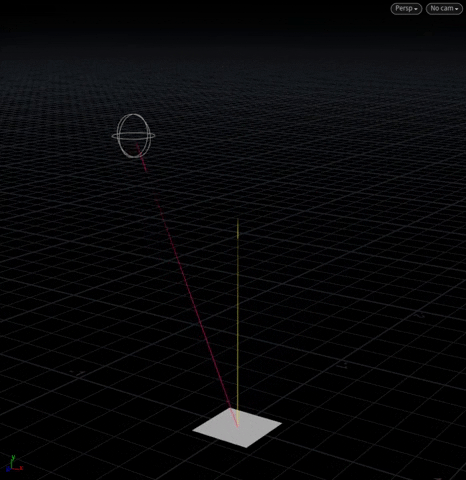
[Above] @N (yellow) is the plane’s normal with a “target vector” (pink) extending from its center to the moving sphere.
Earlier, we learned that the vector between two points A and B is simply B - A. Wrangling the primitive:
v@targetP = point(1, "P", 0); // The position of the moving sphere
v@targetvec = @targetP - @P; // @P is the primitive's "center"
// The matrix that rotates N -> targetvec
matrix3 rot = dihedral(@N, @targetvec);
@N *= rot; // Rotates/aligns N to targetvec -- pointless
@P *= rot; // Useless
Note 1: Rotating a primitive’s @P does nothing to rotate its points. @P is a computed average value (3). And rotating @N simply changes the direction of the normal. Again, the points are unaffected.
Note 2: There’s nothing special about @N. With dihedral, we’re simply saying “take this direction and rotate it to face this other direction”. In our case, the initial direction is {0, 1, 0}, which, for simplicity, we just call @N.
Note 3: Why are we Wrangling the primitive and not the actual points? Because @targetvec is dependent on @P and each point’s position is different, we will end up with 4 different @targetvec-s and 4 different (likely divergent) rotation matrices, which would screw up the shape of the primitive.
What we want is to rotate all the points according to one common frame of reference. To do this, we take the rotation matrix from dihedral and apply it to all the points, using the primitive’s @P as the pivot.
For this, we use instance (still in a Primitive Wrangle, see Note 3):
vector4 orient = dihedral(@N, @targetvec); // dihedral can return both vector4 -- a quaternion -- or a matrix3
4@xform = instance(@P, 0, 1, 0, orient, @P); // declare matrix type attribute
And finally, in a Point Wrangle, we apply the matrix to every point:
matrix xform = prim(0, "xform", 0); // Fetch the matrix from the primitive, or use Attribute Promote
@P *= xform; // Apply
Et voila.
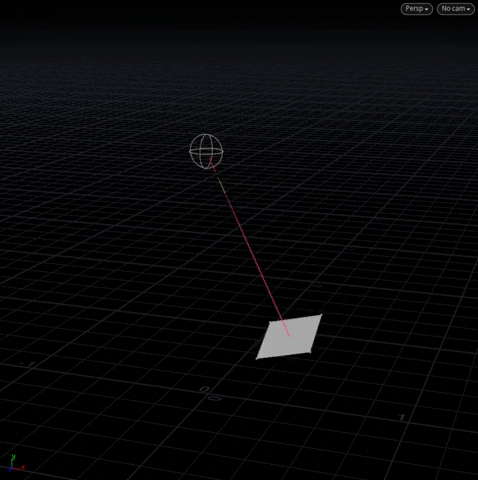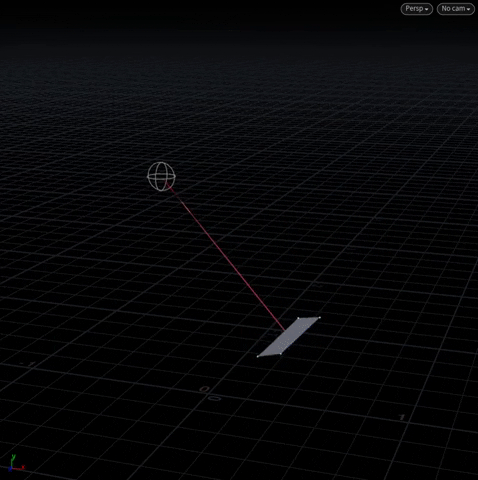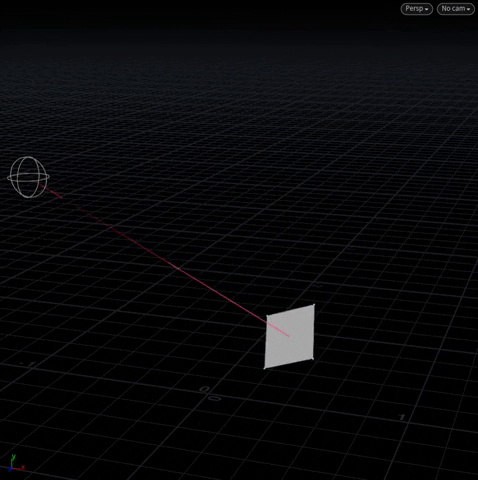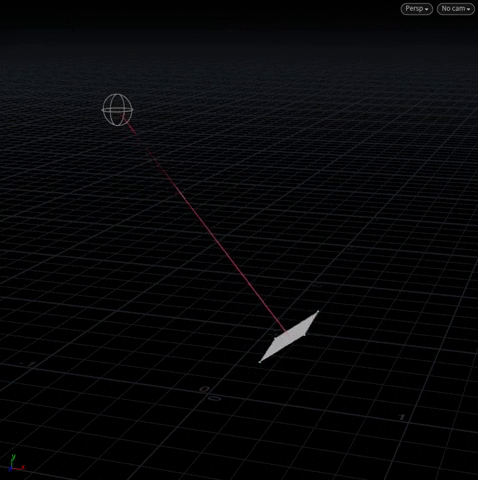
Notice we no longer have to be at the origin. Because we can specify a pivot with instance, we’re free to do transforms anywhere in world space.
Look At with Distance and Slerp
Now let’s do this “look at” thing to the primitives of a faceted grid:

Using distance, the idea is to have a primitive face the target when it’s within a certain radius of the target.
But instead of using distance as an on/off-switch e.g. “to turn or not to turn” – we use it to create a falloff: so the nearer the distance to the target, the more we turn to face it, the further away, etc. until past a certain distance where we stop turning altogether.
If we look at the “target vectors” of what’s happening:

We get this “converging” comb of the vectors, because the vectors at the edge of the “effect radius” turn less vs. the ones at the center.
The function to do this magic is slerp, which gives us a quarternion between two quaternions based on a bias e.g. weight:
vector4 orient_end = dihedral(@N, @targetvec); // same as before
vector4 orient_start = {0,0,0,1}; // an orient that does nothing
slerp(orient_start, orient_end, bias);
As bias approaches 1, the returned quarternion approaches orient_end (e.g. fully facing the target).
At 0, nothing happens.
So now all we gotta do is fit the measured distance into the range 0 <> 1, and use that to control the slerp.