Houdini VEX - Noise and Curves
In these examples, we have a line along +x and we use noise functions to distort it along the y-axis.
Inside a Wrangle over points:
float offset = 0; // This is zero for simplicity
@P.y = sin(@P * @Time + offset);
The combined term of @P * @Time is the frequency of the curves. The higher this number – as @Time increases – the greater the frequency.
We start with the simplest, using sin:
In the subsequent “graphs”, notice the outputs' value ranges.
ax – anoise, xnoise – are between 0 <> 1.
sos – sin, onoise, snoise – are between -1 <> 1. Specifically, o is between -0.5 <> 0.5.
Doc: anoise
Doc: xnoise
Doc: snoise
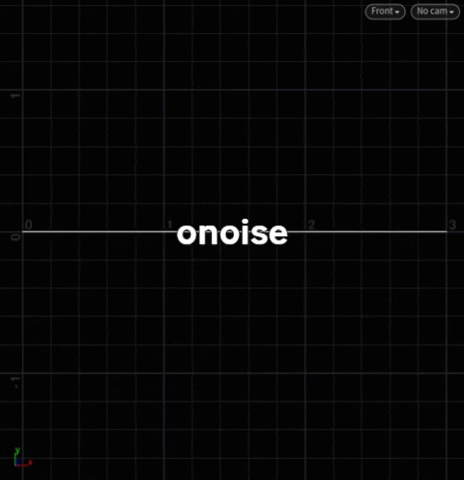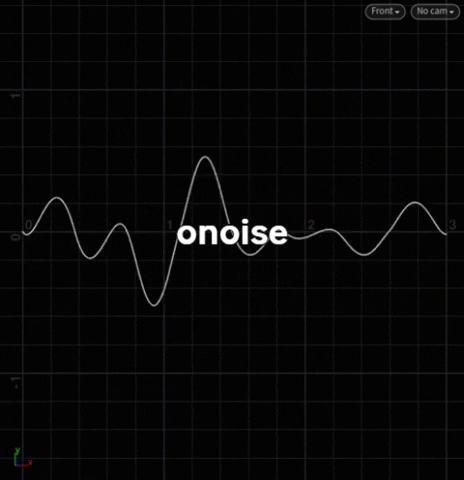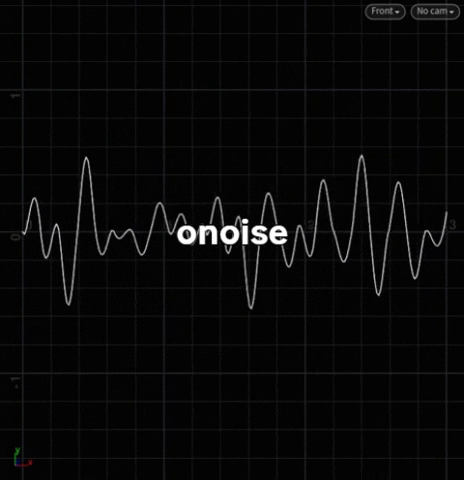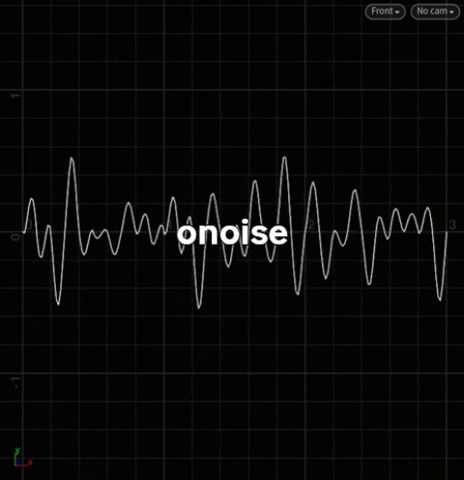Doc: onoise
Regulating noise along a curve
We have a boring line like this:
And we’ll introduce some onoise along it – but we want the noise to “build up” towards the middle of the “wire” and taper off towards the end, the start and end points will be locked.
To do this, we need some factor to regulate how much the noise comes into effect along the curve. We’ll call this “factor” @bias.
So, as the u of the curve moves from 0 -> 1, @bias will move from 0 -> 1 -> 0.
We can use sin or another function for this:
Where x can be @curveu from a Resample SOP.
Now, to do the actual “noising”, we use lerp to interpolate between the initial @P.y and a “noised up” value of @P.y + noise.
float noiz = onoise(@P * 5); // Can also use @P.x, just depends on look
@P.y = lerp(@P.y, @P.y + noiz, @bias);
We use @bias to control this interpolation e.g more in the middle, less in the tail and head, according to the “bell curve” earlier.
And we get this (templating the original line for reference):
