Vectors - Positions and Rotations
- An arbitrary point in space
(x,y,z)is a vector<x,y,z>from the origin.

- Adding a vector
<a,b,c>to a point gives us another point.

- The vector
<a,b,c>can be derived by subtractingP1fromP2.
So far:
vector abc = {1, 2, 3};
vector P2 = P1 + abc;
vector def = P2 - P1; // def == abc
-
The vector
<a,b,c>defines a line in space betweenP1andP2. -
When we normalize a vector e.g. set its length to
1– we essentially discard its original magnitude (length) and leave only a direction.
Normalizing <a,b,c> gives us a direction to “draw a line” from P1 to P2.
- All normalized vectors lie on a unit circle / unit sphere.

- When two points on the surface of a unit sphere
<A> <B>are directly opposite of each other (180°), the vector connecting them<Y>has a length of2.
vector Y = A - B;
float mag = length(Y) // == 2
- The angle
θbetween two vectors from the origin is defined as:

In Vex:
float top = dot(A, B);
float bottom = length(A) * length(B); // if A and B are normalized, this == 1
float angle = acos(top/bottom); // Radians
float fitted = degrees(angle)/180; // Fit to 0<>1. When 0 the lines are parallel, at 1 the lines are perfectly opposed
Cross Product
If we have two points in space:

We can imagine a line that extends from the origin to each point respectively:

Which forms an “imaginary plane”:

The cross product of those two points:
vector P3 = cross(P1, P2);
Gives us a point that is perpendicular (orthoganal) to the imaginary plane created by those two points:

By the right hand rule, changing the order of the points will flip P3’s position:
vector P3 = cross(P2, P1);

The magnitude (length) of the cross product is proportional to the magnitudes of the points along their respectives axes.
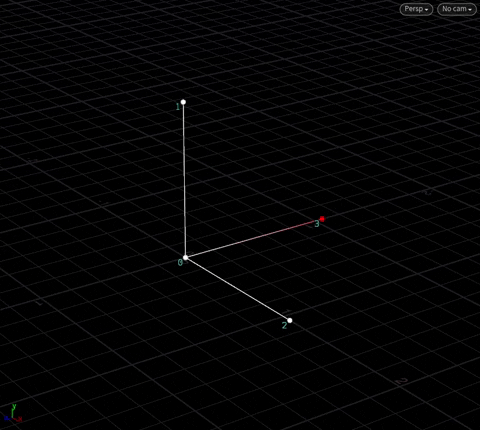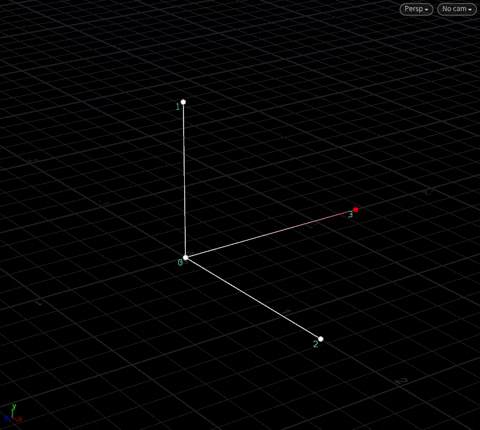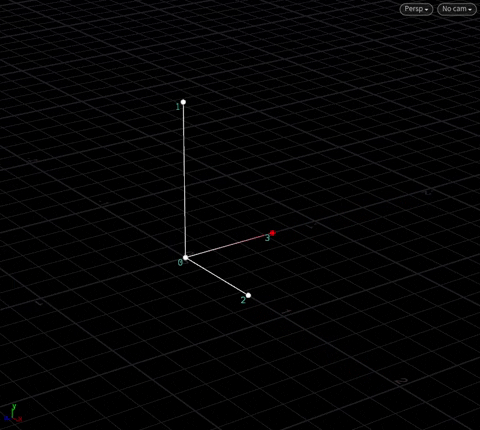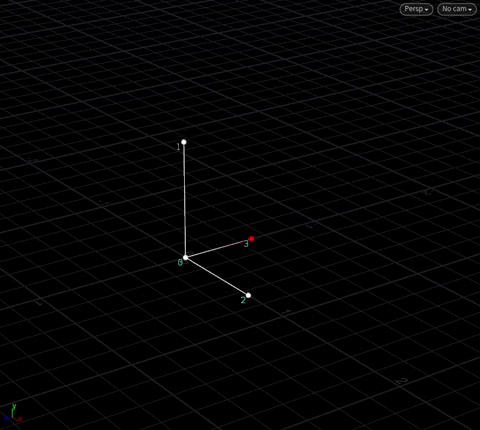
With these three vectors, we now have a “local axis” to do transforms anywhere in space, with point 0 as the origin. In Houdini, we call these axes by their more common names @N, @up, @tangent:

Rotation at the Origin

We have an object at the origin. For the sake of simplicty, we’ll call the three “outside” points N, up and tan, and the “origin” point pivot. Here, tan == cross(up, N) – this is obvious by now.
We want to rotate on the tan axis.
rotate – rotates points with a rotation matrix3, so let’s use that first in a Wrangle over points:
vector axis = tan - pivot; // This was our (3) and (4) "axioms" above
matrix3 m = ident();
rotate(m, radians(angle), axis);
@P *= m;
qrotate – now with a quarternion:
vector axis = tan - pivot;
vector4 qrot = quaternion(radians(angle), axis);
@P = qrotate(qrot, @P);
Both achieve this same thing:
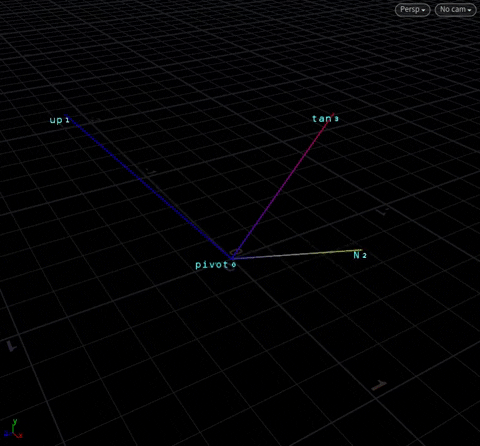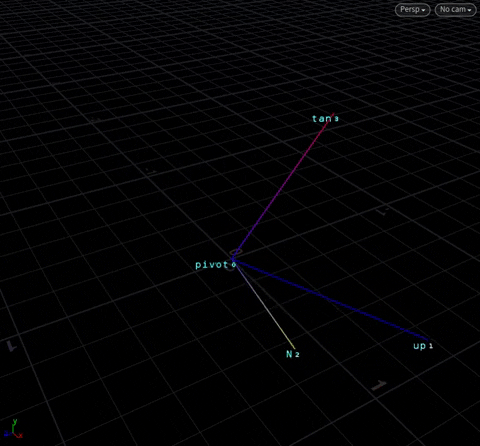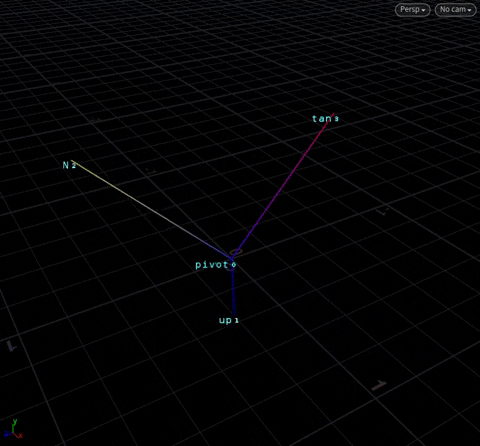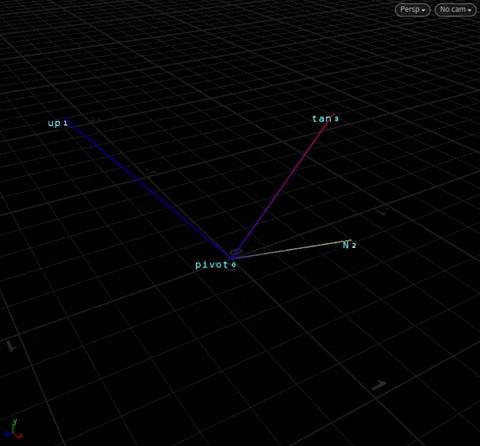
Rotating Anywhere
The function we’ll use to rotate objects anywhere in space is instance – which lets us use the all-powerful @orient to rotate stuff.
Here’s our code, not much different from the one above:
vector axis = tan - pivot;
vector4 qrot = quaternion(radians(angle), axis);
// P, N, scale, post-rotate, orient, pivot
matrix xform = instance(pivot, 0, 1, 0, qrot, pivot); // We ignore N cause we're using orient
@P *= xform;
The crucial element here is the ability to set a new “origin” and pivot point, giving us our own mini “local axis” so we can properly rotate without having to be at the origin.
Also note the only gotcha: even though we’re Wrangling over points, the P parameter is not the point’s @P! Instead we pass in the position from which all points are rotated relative to – aka the pivot.
In our case, we chose pivot as that point. In a more complex object/primitive, this would be the centroid, which we might have to compute by taking the average position of all points on the primitive aka the “origin” of the Normal.